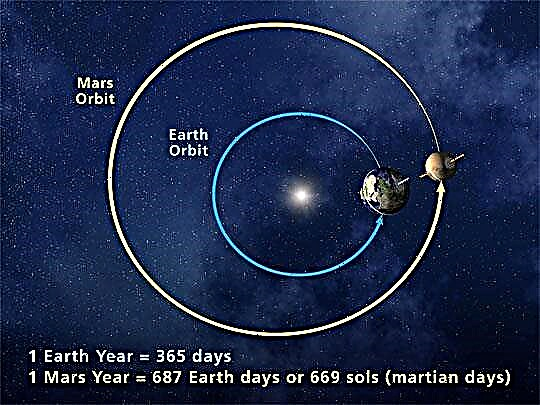
عندما يتعلق الأمر بالفضاء ، تشير كلمة الانحراف دائمًا تقريبًا إلى الانحراف المداري ، أو الانحراف المداري لجسم فلكي ، مثل كوكب أو نجم أو قمر. تكون هذه المدارات بيضاوية الشكل تقريبًا ، والمعلمة الرئيسية التي تصف القطع الناقص هي الانحراف عن المركز.
بعبارات بسيطة ، يكون للمدار الدائري انحراف صفري ، ومدار مكافئ أو نصف قطري انحراف من 1 (إذا كان المدار زائديًا ، فإن انحرافه أكبر من 1) ؛ بالطبع ، إذا كان الانحراف 1 أو أكثر ، فإن "المدار" هو خطأ في التسمية!
في نظام الكواكب الذي يحتوي على أكثر من كوكب واحد (أو لكوكب به أكثر من قمر واحد ، أو نظام نجمي متعدد بخلاف ثنائي) ، تكون المدارات تقريبًا بيضاوية الشكل ، لأن كل كوكب لديه قوة جاذبية على كل كوكب آخر ، و تنتج هذه التسارع مدارات غير إهليلجية. كما أن نمذجة المدارات التي تفترض أن نظرية النسبية العامة تصف الجاذبية تؤدي أيضًا إلى المدارات التي تكون تقريبًا بيضاوية الشكل (وهذا ينطبق بشكل خاص على النجوم النابضة الثنائية).
ومع ذلك ، يتم تلخيص المدارات دائمًا تقريبًا على شكل علامات حذف ، مع وجود الانحراف كواحد من المعلمات المدارية الرئيسية. لماذا ا؟ لأن هذا مريح للغاية ، ولأن الانحرافات عن الحذف يمكن وصفها بسهولة من خلال الاضطرابات الصغيرة.
من السهل نسبيًا كتابة صيغة الانحراف ، في نظام من جسد تحت الجاذبية النيوتونية ، ولكن للأسف ، تتجاوز إمكانات تشفير HTML لصفحة الويب هذه.
ومع ذلك ، إذا كنت تعرف المسافة القصوى للجسم ، من مركز الكتلة - apoapsis (apohelion ، لكواكب النظام الشمسي) ، صأ - والحد الأدنى من هذه المسافة - الحضيض (الحضيض) ، صص - عندئذ يكون الانحراف ، e ، للمدار هو:
E = (صأ - صص) / (صأ+ صص)
لا مركزية المدار (UCAR) ، غريب الأطوار لمدار الأرض (المرصد الشمسي الوطني) ، ومعادلة الوقت (جامعة إلينوي) هي مواقع الويب التي تحتوي على المزيد من الانحراف.
مقالات مجلة الفضاء حول الانحراف؟ أكيد! على سبيل المثال: قياس انحراف القمر في المنزل ، و Buffy the Kuiper Belt Object ، وبحيرة عدم التماثل على تيتان.
حلقتان لصبغ الفلك يكون فيهما الانحراف مهمًا هما نبتون والأرض. تستحق الاستماع إليها.